RAID 1

Source

A RAID 1 creates an exact copy (or mirror) of a set of data on two or more disks. This is useful when read performance or reliability are more important than data storage capacity. Such an array can only be as big as the smallest member disk. A classic RAID 1 mirrored pair contains two disks (see diagram), which increases reliability geometrically over a single disk. Since each member contains a complete copy of the data, and can be addressed independently, ordinary wear-and-tear reliability is raised by the power of the number of self-contained copies.
RAID 1 failure rate
As a trivial example, consider a RAID 1 with two identical models of a disk drive with a 5% probability that the disk would fail within three years. Provided that the failures are statistically independent, then the probability of both disks failing during the three year lifetime is

.

Thus, the probability of losing all data is 0.25% if the first failed disk is never replaced. If only one of the disks fails, no data would be lost, assuming the failed disk is replaced before the second disk fails.

However, since two identical disks are used and since their usage patterns are also identical, their failures can not be assumed to be independent. Thus, the probability of losing all data, if the first failed disk is not replaced, is considerably higher than 0.25% but still below 5%.

---

RAID 0 failure rate
Reliability of a given RAID 0 set is equal to the average reliability of each disk divided by the number of disks in the set:

That is, reliability (as measured by mean time to failure (MTTF) or mean time between failures (MTBF) is roughly inversely proportional to the number of members – so a set of two disks is roughly half as reliable as a single disk. If there were a probability of 5% that the disk would fail within three years, in a two disk array, that probability would be upped to .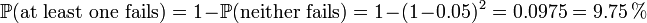

The reason for this is that the file system is distributed across all disks. When a drive fails the file system cannot cope with such a large loss of data and coherency since the data is "striped" across all drives (the data cannot be recovered without the missing disk). Data can be recovered using special tools, however, this data will be incomplete and most likely corrupt, and recovery of drive data is very costly and not guaranteed.

---

RAID 1 performance
Since all the data exists in two or more copies, each with its own hardware, the read performance can go up roughly as a linear multiple of the number of copies. That is, a RAID 1 array of two drives can be reading in two different places at the same time, though not all implementations of RAID 1 do this.^[5] To maximize performance benefits of RAID 1, independent disk controllers are recommended, one for each disk. Some refer to this practice as splitting or duplexing. When reading, both disks can be accessed independently and requested sectors can be split evenly between the disks. For the usual mirror of two disks, this would, in theory, double the transfer rate when reading. The apparent access time of the array would be half that of a single drive. Unlike RAID 0, this would be for all access patterns, as all the data are present on all the disks. In reality, the need to move the drive heads to the next block (to skip blocks already read by the other drives) can effectively mitigate speed advantages for sequential access. Read performance can be further improved by adding drives to the mirror. Many older IDE RAID 1 controllers read only from one disk in the pair, so their read performance is always that of a single disk. Some older RAID 1 implementations would also read both disks simultaneously and compare the data to detect errors. The error detection and correction on modern disks makes this less useful in environments requiring normal availability. When writing, the array performs like a single disk, as all mirrors must be written with the data. Note that these performance scenarios are in the best case with optimal access patterns.
RAID 1 has many administrative advantages. For instance, in some environments, it is possible to "split the mirror": declare one disk as inactive, do a backup of that disk, and then "rebuild" the mirror. This is useful in situations where the file system must be constantly available. This requires that the application supports recovery from the image of data on the disk at the point of the mirror split. This procedure is less critical in the presence of the "snapshot" feature of some file systems, in which some space is reserved for changes, presenting a static point-in-time view of the file system. Alternatively, a new disk can be substituted so that the inactive disk can be kept in much the same way as traditional backup. To keep redundancy during the backup process, some controllers support adding a third disk to an active pair. After a rebuild to the third disk completes, it is made inactive and backed up as described above.